Gravitace

Vojtěch Svoboda

Cíle:

1. Poznáte zákony pohybu planet, které na počátku 17. století objevil J. Kepler.
2. Seznámíte se s Newtonovým zákonem gravitace a pojmem gravitační pole.
3. Naučíte se používat gravitační zákon i Keplerovy zákony k řešení mnoha
úloh, například o pohybu planet kolem slunce či pohybu družic kolem
Země.
4. Dozvíte se, jak vypadá tíhové pole Země a také jak se gravitace projevuje v na-
šem vesmíru.

Entree

Kepplerovy zákony

Johannes Kepler

žil v letech 1571 – 1630 astronom, matematik, astrolog několik let působil na dvoře císaře Rudolfa II. v Praze, kde také zformuloval dva ze tří jeho zákonů počeštěná forma jeho jména: Jan Kepler

1. Kepplerův zákon

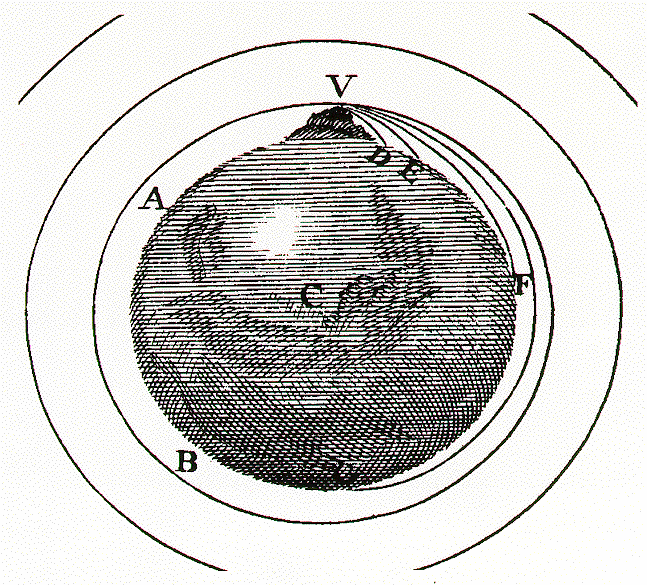
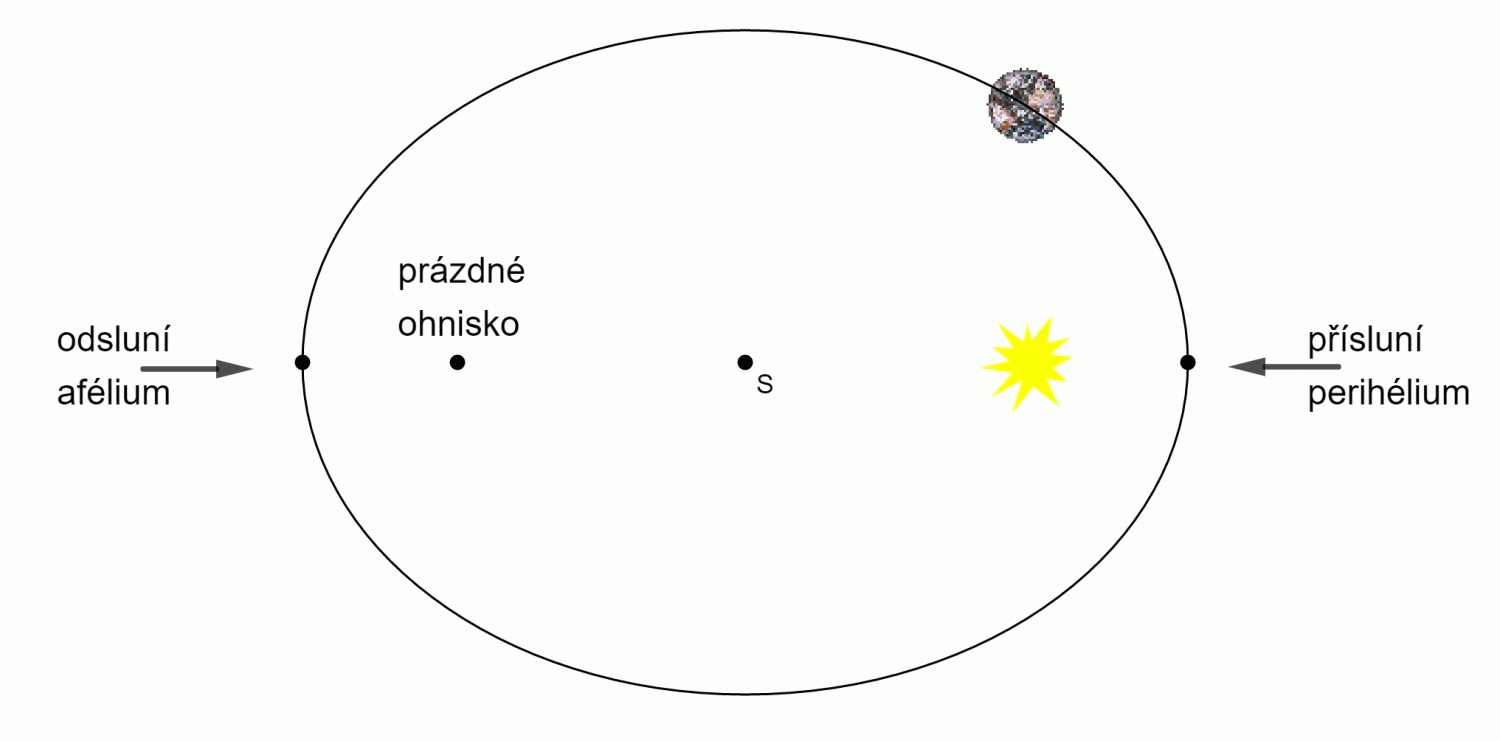
Planety obíhají kolem Slunce po eliptických drahách (přesněji trajektoriích), v jejichž jednom společném ohnisku je Slunce.

• Popisuje trajektorie planet.
• Planety se periodicky vzdalují a přibližují ke Slunci.
• Roviny drah všech planet procházejí středem Slunce, jsou přibližně totožné. Slunce se nachází v ohnisku dráhy každé planety.
• Planety obíhají kolem Slunce, takže geocentrický popis nebeské mechaniky již není vhodný.

Elipsa

Animace

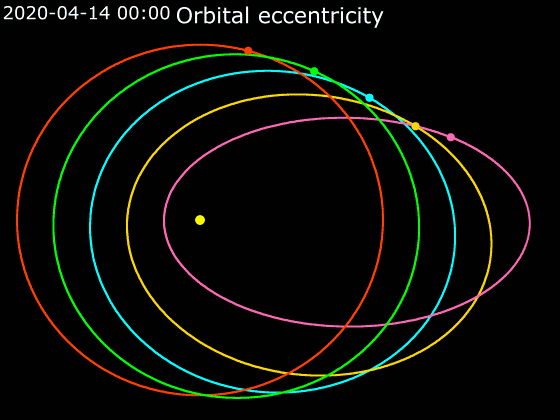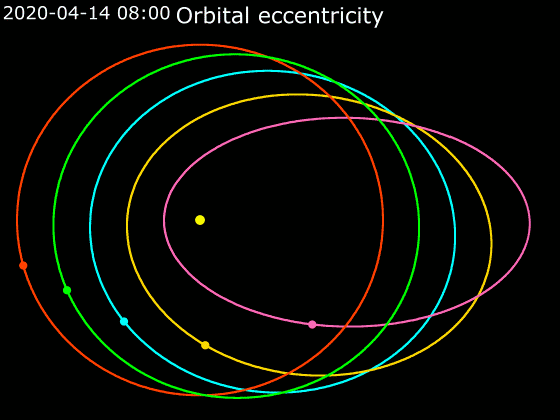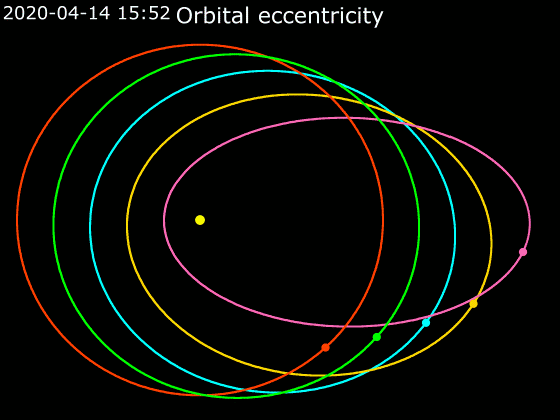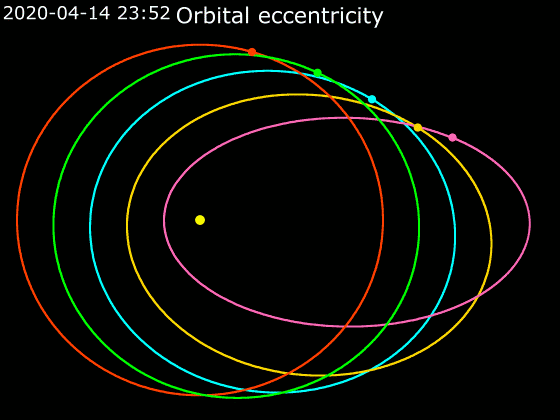
2. Kepplerův zákon

Obsahy ploch opsaných průvodičem planety (spojnice planety a Slunce) za stejný čas jsou stejně velké

• Popisuje rychlosti planet (komet, planetek) obíhajících Slunce
• Čím blíže je planeta u Slunce, tím se rychleji pohybuje.

3. Kepplerův zákon

Poměr druhých mocnin oběžných dob dvou planet je stejný jako poměr třetích mocnin délek jejich hlavních poloos (středních vzdáleností těchto planet od Slunce).

Pokud označíme \(T_1\) a \(T_2\) oběžné doby dvou planet a \(a_1\) a \(a_2\) délky jejich hlavních poloos, pak lze tento zákon vyjádřit ve tvaru:\[T_1^2/T_2^2=a_1^3/a_2^3\]

Tento zákon platí v tomto tvaru jen tehdy, jsou-li hmotnosti planet zanedbatelně malé ve srovnání s hmotností Slunce, což je u planet Sluneční soustavy splněno.

Zdroje

• Přispěvatelé Wikipedie, „Keplerovy zákony,“ Wikipedie: Otevřená encyklopedie, Link (získáno 31. 10. 2024).
• Wikipedia contributors, “Kepler’s laws of planetary motion,” Wikipedia, The Free Encyclopedia, Link (accessed October 31, 2024).
• Tomáš Nečas: Fyzika pro gymnázia - Mechanika. 2008.

Chicago style