Gravitace

Vojtěch Svoboda

Cíle:

1. Poznáte zákony pohybu planet, které na počátku 17. století objevil J. Kepler.
2. Seznámíte se s Newtonovým zákonem gravitace a pojmem gravitační pole.
3. Naučíte se používat gravitační zákon i Keplerovy zákony k řešení mnoha
úloh, například o pohybu planet kolem slunce či pohybu družic kolem
Země.
4. Dozvíte se, jak vypadá tíhové pole Země a také jak se gravitace projevuje v na-
šem vesmíru.

Entreé

Kepplerovy zákony

Johannes Kepler

žil v letech 1571 – 1630 astronom, matematik, astrolog několik let působil na dvoře císaře Rudolfa II. v Praze, kde také zformuloval dva ze tří jeho zákonů počeštěná forma jeho jména: Jan Kepler

1. Kepplerův zákon

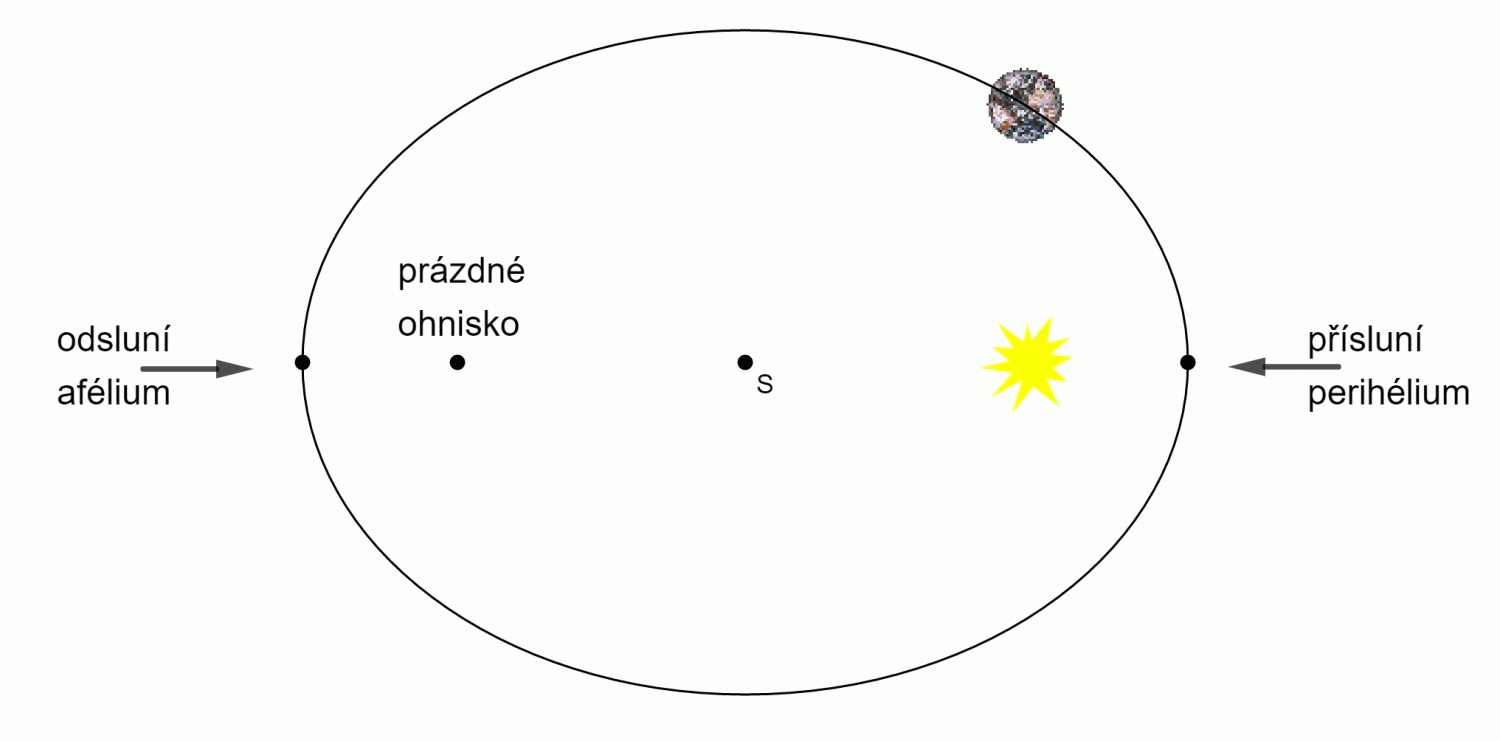
Planety obíhají kolem Slunce po eliptických drahách (přesněji trajektoriích), v jejichž jednom společném ohnisku je Slunce.

• Popisuje trajektorie planet.
• Planety se periodicky vzdalují a přibližují ke Slunci.
• Roviny drah všech planet procházejí středem Slunce, jsou přibližně totožné. Slunce se nachází v ohnisku dráhy každé planety.
• Planety obíhají kolem Slunce, takže geocentrický popis nebeské mechaniky již není vhodný.

Elipsa

Animace

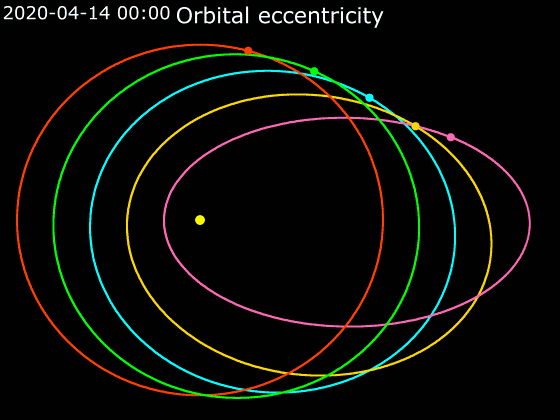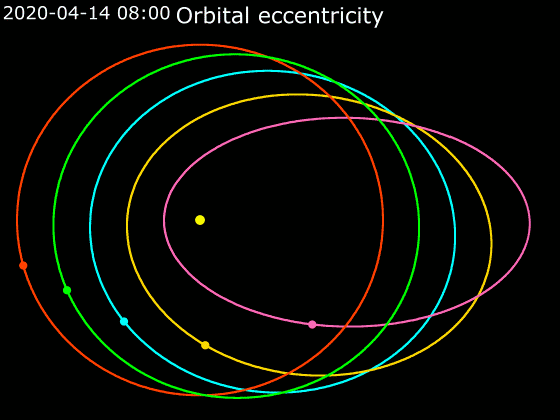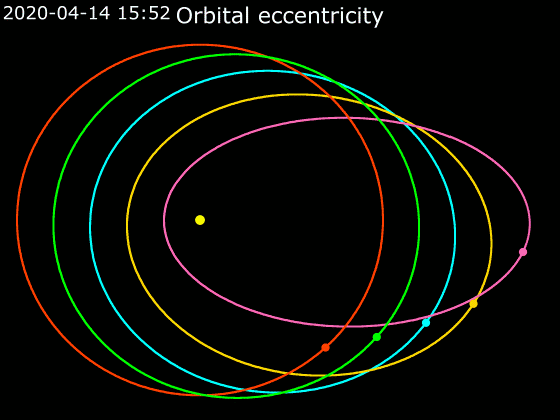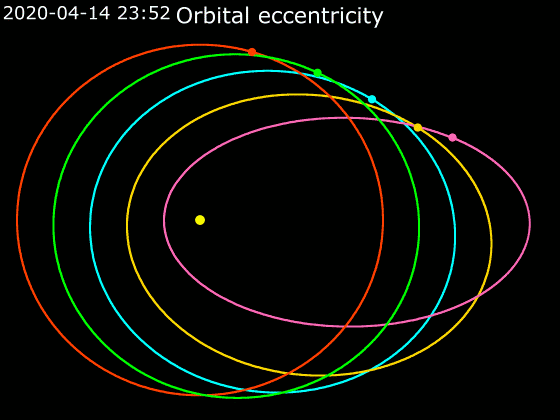
2. Kepplerův zákon

Obsahy ploch opsaných průvodičem planety (spojnice planety a Slunce) za stejný čas jsou stejně velké

• Popisuje rychlosti planet (komet, planetek) obíhajících Slunce
• Čím blíže je planeta u Slunce, tím se rychleji pohybuje.

3. Kepplerův zákon

Poměr druhých mocnin oběžných dob dvou planet je stejný jako poměr třetích mocnin délek jejich hlavních poloos (středních vzdáleností těchto planet od Slunce).

Pokud označíme \(T_1\) a \(T_2\) oběžné doby dvou planet a \(a_1\) a \(a_2\) délky jejich hlavních poloos, pak lze tento zákon vyjádřit ve tvaru:\[T_1^2/T_2^2=a_1^3/a_2^3\]

Tento zákon platí v tomto tvaru jen tehdy, jsou-li hmotnosti planet zanedbatelně malé ve srovnání s hmotností Slunce, což je u planet Sluneční soustavy splněno.

Newtonův gravitační zákon

Zákon

• Jablko ze stromu a stejně tak všechna ostatní tělesa padají, protože je Země přitahuje. Nemělo by půosbení této přitažlivé síly pokračovat mnohem dál až k Měsíci?
• Podlunární a nadlunární mechanika.
• Newton matematicky odvodil, že pohybuje-li se planeta po elipse podle tří Keplerových zákonů, musí na ni Slunce působit silou, jejíž velikost je nepřímo úměrná druhé mocnicně vzdálenosti \(r\) Slunce a planety

• Odvodil obecný vztah pro gravitační sílu, který dnes nazýváme Newtonův gravitační zákon. Ten říká, že dva hmotné body o hmot- nostech \(m_1\), \(m_2\) ve vzdálenosti \(r\) se vzájemně přitahují gravitační silou o velikosti \[F_g = G \cdot (m_1\cdot m_2 / r^2)\] kde \(G=6,67\cdot10^{11} Nm^2kg^{-2}\). Hodnota gravitační konstanty určuje velikost gravitační síly pro dvě konkrétní částice v určité vzdálenosti..
• Například dvě kilogramová závaží ve vzdálenosti jeden metr, vyjde nám, že na sebe budou působit gravitační silou o velikosti \(F_G =6,67\cdot10^{11} N\). To je tak malá síla, že ji ani nedokážeme změřit.
• Gravitační zákon v uvedeném tvaru platí přesně jen pro hmotné body. Ale dá se dokázat, že gravitační zákon platí úplně stejně i pro kulová tělesa jako jsou planety a hvězdy (obecně sféricky symetrická tělesa).

Země a měsíc

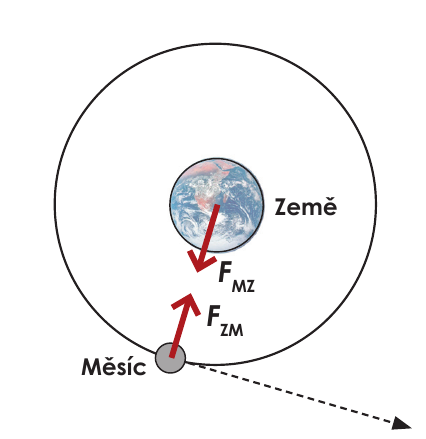
Země a objekt (třeba člověk)

\[F_G = G \cdot (m_Z\cdot m / r_Z^2) = (G \cdot m_Z/ r_Z^2)\cdot m = g\cdot m\]

• Velikost gravitačního zrychlení \(g = G \cdot m_Z/ r_Z^2 = ??\)

Cavendishův experiment (Zvážení Země)

Gravitační pole

• Chceme-li zjistit, jak vypadá gravitační pole nějakého hmotného tělesa o hmotnosti \(M\) (například Země).
• Vezmeme malé zkušební těleso o hmotnosti \(m\) (například závaží) a umístíme jej do libovolného bodu prostoru.
• pak \(a_G=F_g/m = G\cdot M/r^2\)
• Pro vlastnostmi gravitačního pole Země platí: \(a_G= G\cdot M_Z/r_Z^2=9.8\) m, s\(^{-2}\)
• Nezávislé na hmotnosti!

Experiment pírko a kladivo

Závislost na vzdálenosti

• Budeme-li se od Země vzdalovat, bude gravitační zrychlení klesat s druhou mocninou vzdálenosti od středu Země

Tíhové pole Země

Korekce gravitačního pole v reálném prostředí Země

Rotace

• Musíme to ještě zpřesnit. Není to všude stejné. Nenaměřili bychom všude svoji stejnou hmotnost.
• Míchá se do toho rotace Země.
• Zatím máme, že gravitační zrychlení na povrchu Země je \(a_G = 9,83\) m, s\(^{-2}\).

Situace člověka, stojícího na váze, který se nachází na rovníku.

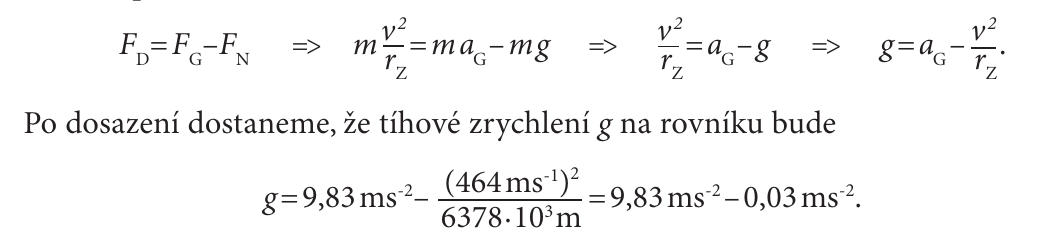
+ zploštění

• Kromě rotace Země má na místní tíhové zrychlení vliv ještě nepravidelný tvar Země.
• Planeta je mírně zploštělá, vzdálenost ke středu Země na rovníku je 6378 km zatímco na pólech jen 6357 km.

Finále

• Hodnoty tíhového zrychlení se pohybují mezi g= 9,78 m, s\(^{-2}\) na rovníku a g=9,83 m, s\(^{-2}\) na pólech.

Pohyb těles v gravitačním poli Země

V blízkosti povrchu Země (podlunární mechanika)

• Tělesa se nachází v homogenním gravitačním poli -> přímočarý (volný pád) a křivočarý pohyb (šikmý vrh).
• Přímka nebo části paraboly.

Pohyb těles ve větší vzdálenosti od povrchu Země, v centrálním gravitačním poli.

• Pohyb družic

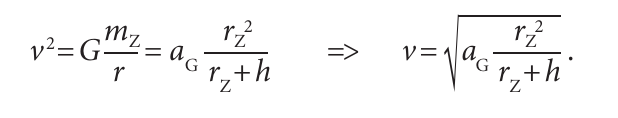
První kosmická rychlost

• Dosadíme \(h=0\) - > \(v=7.9\) km/s

Druhá kosmická rychlost

• \(v_{2K}=\sqrt{2}*v_{1K}=11.2\) km/s

Typy pohybů v gravitačním poli podle počáteční rychlosti \(v_i\) rovnobežně s povrchem Země.

• \(v_i=0\) Volný pád (neperiodický)
• \(0<v_i<v_{1K}\) Vodorovný vrh (neperiodický s pádem)
• \(0<v_i<v_{1K}\) Kruhový v urřité výšce nad povrchem Země (periodický)
• \(v_i=v_{1K}\) Kruhový na povrchu Země, periodický
• \(v_{1K}<v_i<v_{2K}\) Eliptický, periodický
• \(v_i>v_{2K}\) Parabolický, neperidický

Newtonův kanón

Zajímavosti

Urychlování sond

Transportní tunel

Zdroje

• Přispěvatelé Wikipedie, „Keplerovy zákony,“ Wikipedie: Otevřená encyklopedie, Link (získáno 31. 10. 2024).
• Wikipedia contributors, “Kepler’s laws of planetary motion,” Wikipedia, The Free Encyclopedia, Link (accessed October 31, 2024).
• Tomáš Nečas: Fyzika pro gymnázia - Mechanika. 2008.
• Wikipedia contributors, “Newton’s law of universal gravitation,” Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Newton%27s_law_of_universal_gravitation&oldid=1254014824 (accessed October 31, 2024).

Chicago style