---
format:markdown
...
# Gravitace
Vojtěch Svoboda
 ## Cíle:
## Cíle:
1. Poznáte zákony pohybu planet, které na počátku 17. století objevil J. Kepler.
2. Seznámíte se s Newtonovým zákonem gravitace a pojmem gravitační pole.
3. Naučíte se používat gravitační zákon i Keplerovy zákony k řešení mnoha
úloh, například o pohybu planet kolem slunce či pohybu družic kolem
Země.
4. Dozvíte se, jak vypadá tíhové pole Země a také jak se gravitace projevuje v na-
šem vesmíru.
 # Entreé
## Geocentrismus vs. heliocentrismus
# Kepplerovy zákony
# Johannes Kepler
# Entreé
## Geocentrismus vs. heliocentrismus
# Kepplerovy zákony
# Johannes Kepler

|
- žil v letech 1571 – 1630
- astronom, matematik, astrolog
- několik let působil na dvoře císaře
Rudolfa II. v Praze, kde také zformuloval
dva ze tří jeho zákonů
- počeštěná forma jeho jména: Jan Kepler
|
# 1. Kepplerův zákon
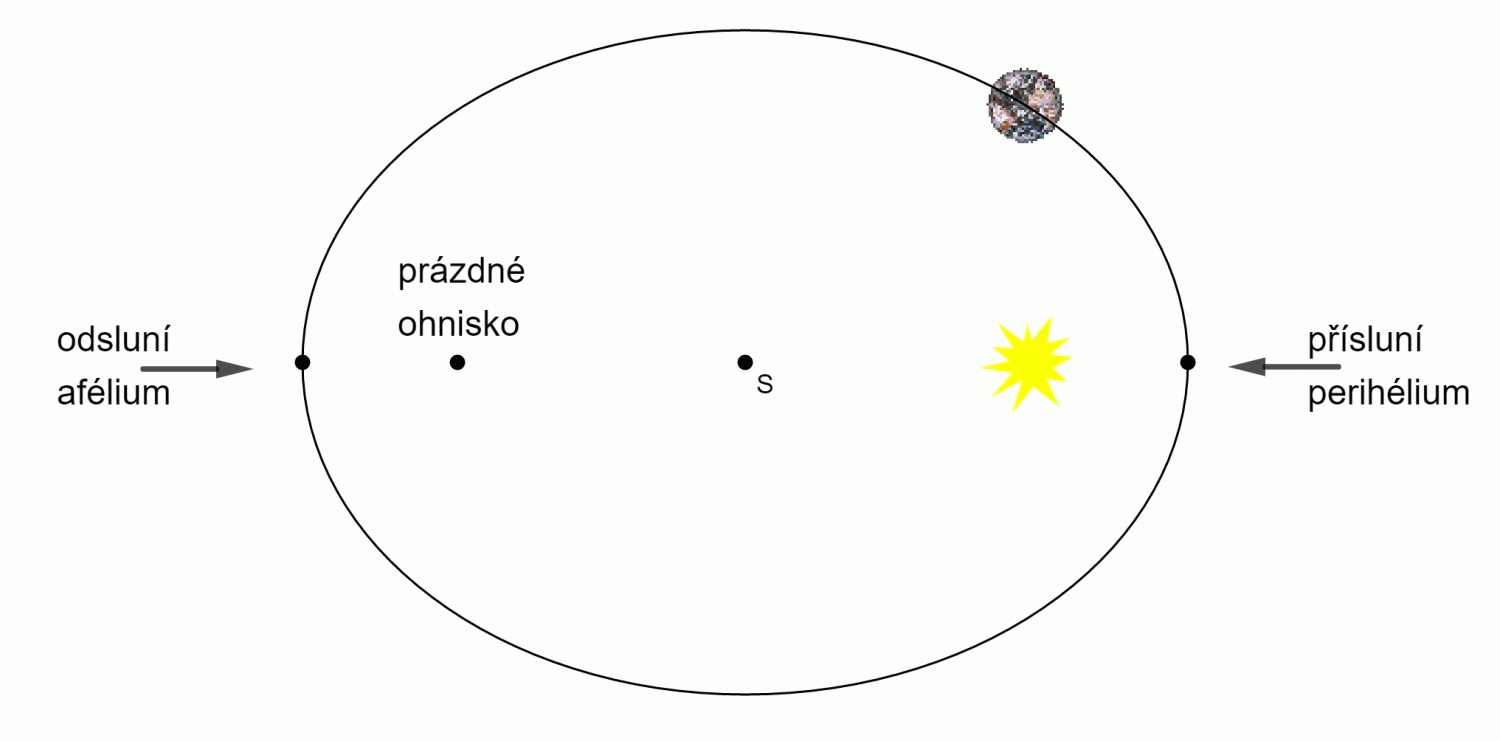
**Planety obíhají kolem Slunce po eliptických drahách (přesněji trajektoriích), v jejichž jednom společném ohnisku je Slunce.**
* Popisuje trajektorie planet.
* Planety se periodicky vzdalují a přibližují ke Slunci.
* Roviny drah všech planet procházejí středem Slunce, jsou přibližně totožné. Slunce se nachází v ohnisku dráhy každé planety.
* Planety obíhají kolem Slunce, takže geocentrický popis nebeské mechaniky již není vhodný.
## Elipsa
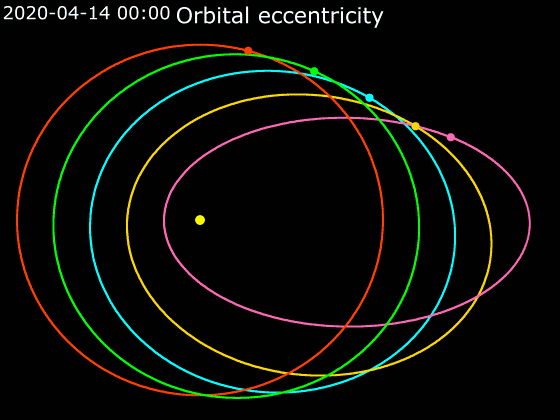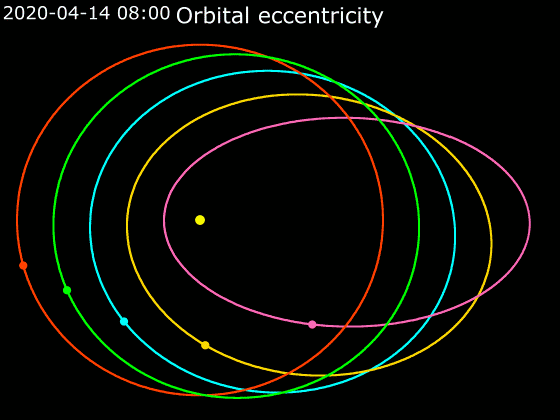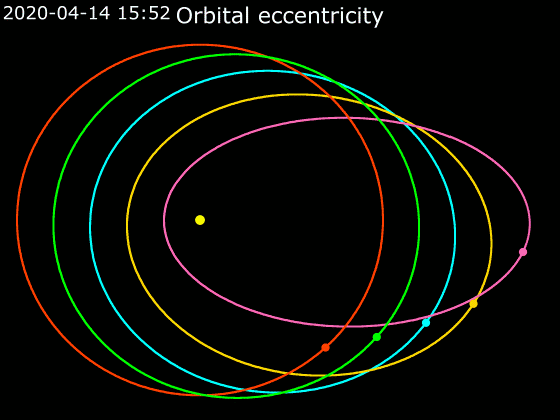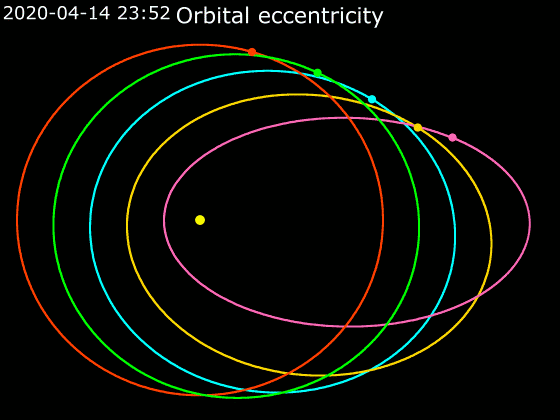
 ## Animace
## Animace
 # 2. Kepplerův zákon
**Obsahy ploch opsaných průvodičem planety (spojnice planety a Slunce) za stejný čas jsou stejně velké**
* Popisuje rychlosti planet (komet, planetek) obíhajících Slunce
* Čím blíže je planeta u Slunce, tím se rychleji pohybuje.
# 2. Kepplerův zákon
**Obsahy ploch opsaných průvodičem planety (spojnice planety a Slunce) za stejný čas jsou stejně velké**
* Popisuje rychlosti planet (komet, planetek) obíhajících Slunce
* Čím blíže je planeta u Slunce, tím se rychleji pohybuje.
 # 3. Kepplerův zákon
**Poměr druhých mocnin oběžných dob dvou planet je stejný jako poměr třetích mocnin délek jejich hlavních poloos (středních vzdáleností těchto planet od Slunce).**
Pokud označíme $T_1$ a $T_2$ oběžné doby dvou planet a $a_1$ a $a_2$ délky jejich hlavních poloos, pak lze tento zákon vyjádřit ve tvaru:$$T_1^2/T_2^2=a_1^3/a_2^3$$
# 3. Kepplerův zákon
**Poměr druhých mocnin oběžných dob dvou planet je stejný jako poměr třetích mocnin délek jejich hlavních poloos (středních vzdáleností těchto planet od Slunce).**
Pokud označíme $T_1$ a $T_2$ oběžné doby dvou planet a $a_1$ a $a_2$ délky jejich hlavních poloos, pak lze tento zákon vyjádřit ve tvaru:$$T_1^2/T_2^2=a_1^3/a_2^3$$
 Tento zákon platí v tomto tvaru jen tehdy, jsou-li hmotnosti planet zanedbatelně malé ve srovnání s hmotností Slunce, což je u planet Sluneční soustavy splněno.
Tento zákon platí v tomto tvaru jen tehdy, jsou-li hmotnosti planet zanedbatelně malé ve srovnání s hmotností Slunce, což je u planet Sluneční soustavy splněno.
 # Newtonův gravitační zákon
* Newton matematicky odvodil, že pohybuje-li se planeta po elipse podle tří Keplerových zákonů, musí na ni Slunce působit silou, jejíž velikost je nepřímo úměrná druhé mocnicně vzdálenosti $r$ Slunce a planety
# Newtonův gravitační zákon
* Newton matematicky odvodil, že pohybuje-li se planeta po elipse podle tří Keplerových zákonů, musí na ni Slunce působit silou, jejíž velikost je nepřímo úměrná druhé mocnicně vzdálenosti $r$ Slunce a planety
 * Odvodil obecný vztah pro gravitační sílu, který dnes
nazýváme Newtonův gravitační zákon. Ten říká, že dva hmotné body o hmot-
nostech $m_1$, $m_2$ ve vzdálenosti $r$ se vzájemně přitahují gravitační silou o velikosti
$$F_g = G \cdot (m_1\cdot m_2 / r^2)$$
kde $G=6,67\cdot10^{11} Nm^2kg^{-2}$. Hodnota gravitační konstanty určuje velikost gravitační síly pro dvě konkrétní částice v určité vzdálenosti..
* Například dvě kilogramová závaží ve vzdálenosti jeden metr, vyjde nám, že na sebe budou působit gravitační silou o velikosti $F_G =6,67\cdot10^{11} N$. To je tak malá síla, že ji ani nedokážeme změřit.
* Odvodil obecný vztah pro gravitační sílu, který dnes
nazýváme Newtonův gravitační zákon. Ten říká, že dva hmotné body o hmot-
nostech $m_1$, $m_2$ ve vzdálenosti $r$ se vzájemně přitahují gravitační silou o velikosti
$$F_g = G \cdot (m_1\cdot m_2 / r^2)$$
kde $G=6,67\cdot10^{11} Nm^2kg^{-2}$. Hodnota gravitační konstanty určuje velikost gravitační síly pro dvě konkrétní částice v určité vzdálenosti..
* Například dvě kilogramová závaží ve vzdálenosti jeden metr, vyjde nám, že na sebe budou působit gravitační silou o velikosti $F_G =6,67\cdot10^{11} N$. To je tak malá síla, že ji ani nedokážeme změřit.
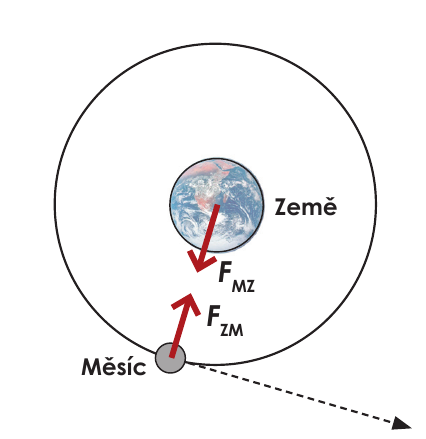 Kdybychom gravitaci „vypnuli“, Měsíc by podle zákona setrvačnosti pokračoval
v rovnoměrném pohybu v daném směru a od Země by se odpoutal. Gravitační síla je v tomto případě dostředivou silou.
# Zdroje
* Přispěvatelé Wikipedie, „Keplerovy zákony,“ Wikipedie: Otevřená encyklopedie, Link (získáno 31. 10. 2024).
* Wikipedia contributors, "Kepler's laws of planetary motion," Wikipedia, The Free Encyclopedia, Link (accessed October 31, 2024).
* Tomáš Nečas: Fyzika pro gymnázia - Mechanika. 2008.
*Chicago style*
Kdybychom gravitaci „vypnuli“, Měsíc by podle zákona setrvačnosti pokračoval
v rovnoměrném pohybu v daném směru a od Země by se odpoutal. Gravitační síla je v tomto případě dostředivou silou.
# Zdroje
* Přispěvatelé Wikipedie, „Keplerovy zákony,“ Wikipedie: Otevřená encyklopedie, Link (získáno 31. 10. 2024).
* Wikipedia contributors, "Kepler's laws of planetary motion," Wikipedia, The Free Encyclopedia, Link (accessed October 31, 2024).
* Tomáš Nečas: Fyzika pro gymnázia - Mechanika. 2008.
*Chicago style*
 ## Cíle:
## Cíle:


 ## Animace
## Animace



 Kdybychom gravitaci „vypnuli“, Měsíc by podle zákona setrvačnosti pokračoval
v rovnoměrném pohybu v daném směru a od Země by se odpoutal. Gravitační síla je v tomto případě dostředivou silou.
Kdybychom gravitaci „vypnuli“, Měsíc by podle zákona setrvačnosti pokračoval
v rovnoměrném pohybu v daném směru a od Země by se odpoutal. Gravitační síla je v tomto případě dostředivou silou.